Protein-Protein Interaction Graphs¶
More about R¶
In previous practicals you have have used the R statistics software for analysing many different types of data. In this practical, you will use R for analysing protein-protein interaction data. However, first we will discuss some features of R that will be useful in this practical.
One thing that is useful to know about R is that many R packages come with example data sets, which can be used to familiarise yourself with the functions in the particular package. To list the data sets that come with a particular package, you can use the data() function in R. For example, to find the data sets that come with the “graph” package, type:
> library("graph")
> data(package="graph")
Data sets in package 'graph':
IMCAAttrs (integrinMediatedCellAdhesion)
KEGG Integrin Mediated Cell Adhesion graph
IMCAGraph (integrinMediatedCellAdhesion)
KEGG Integrin Mediated Cell Adhesion graph
MAPKsig A graph encoding parts of the MAPK signaling pathway
MAPKsig (defunctGraph) A graph encoding parts of the MAPK signaling pathway
apopGraph KEGG apoptosis pathway graph
biocRepos A graph representing the Bioconductor package repository
graphExamples A List Of Example Graphs
pancrCaIni A graph encoding parts of the pancreatic cancer initiation
You can then load any of these data sets into R by typing, for example, to load the apopGraph data set:
> data("apopGraph")
In this practical, you will also be using the table() function to make tables of data stored in vectors. If you have a vector containing numeric values, the table() function is useful for making a table saying how many elements in the vector have each of the values. For example:
> y <- c(10, 10, 20, 20, 20, 20, 20, 30) # Make a numeric vector "y"
> table(y)
y
10 20 30
2 5 1
The results from the table() function tell us that two of the elements in vector y have values of 10, five elements have values of 20, and one element has a value of thirty.
Another use of the table() function is to tell us how many elements in a vector of numbers have a particular numeric value. For example, if we want to know how many elements in vector y have a value of 20, we can type:
> table(y == 20)
FALSE TRUE
3 5
This tells us that five elements of vector y have values of 20.
In this practical you will be using functions from several different packages. It’s important to remember that sometimes functions in different packages have the same name. For example, there is a function called degree() in both the “igraph” and “graph” packages. Therefore, you need to specify which degree() function you want to use, by putting the package name, followed by ”:”, before the name of the function. For example, to use the degree() function from the “graph” package, you can type graph::degree(), while to use the degree() function from the “igraph” package, you can type igraph::degree().
Graphs for protein-protein interaction data in R¶
Protein-protein interaction data can be described in terms of graphs. In this practical, we will explore a curated data set of protein-protein interactions, by using R packages for analysing and visualising graphs.
We will use three main R packages that have been written for handling biological graphs: the “graph” package, the “RBGL” package, and the “Rgraphviz” package. The Rgraphviz package is part of the Bioconductor set of R packages, so needs to be installed as part of that set of package (see the Bioconductor webpage at www.bioconductor.org/docs/install/ for details).
We will first analyse a curated data set of protein-protein interactions in the yeast Saccharomyces cerevisiae extracted from published papers. This data set comes from with an R package called “yeastExpData”, which calls the data set “litG”. This data was first described in a paper by Ge et al (2001) in Nature Genetics (http://www.nature.com/ng/journal/v29/n4/full/ng776.html).
To read the litG data set into R, we first need to load the yeastExpData package, and then we can use the R data() function to read in the litG data set:
> library("yeastExpData") # Load the yeastExpData package
> data("litG") # Read the litG data set
When you read in the litG data set using the data() function, it is stored as a graph in R. In this graph, the vertices (nodes) are proteins, and edges between vertices indicate that two proteins interact. There are 2885 different vertices in the graph, representing 2885 different proteins.
You can print out the number of vertices and edges in a graph in R by just typing the name of the graph, for example:
> litG
A graphNEL graph with undirected edges
Number of Nodes = 2885
Number of Edges = 315
This tells us that the litG graph has 2885 vertices, and 315 edges. The 315 edges in the graph represent 315 protein-protein interactions between 315 pairs of proteins.
Finding the names of vertices in graphs for protein-protein interaction data in R¶
The “graph” R package contains many functions for analysing graph data in R. For example, the nodes() function from the graph package can be used to retrieve the names of the vertices (nodes) in the graph. For example, we can retrive the names of the vertices in the litG graph, and store them in a vector “mynodes”, by typing:
> library("graph") # Load the graph package
> mynodes <- nodes(litG) # Retrieve the names of the vertices in the litG graph
We can then print the names of the first 10 vertices in the litG graph, by typing:
> mynodes[1:10] # Print the names of the first 10 vertices in the litG graph
[1] "YBL072C" "YBL083C" "YBR009C" "YBR010W" "YBR031W" "YBR093C" "YBR106W"
[8] "YBR118W" "YBR188C" "YBR191W"
This gives the names of the yeast proteins corresponding to the first 10 vertices in the litG graph. Note that the order that the proteins are stored in the graph does not have any meaning; these 10 proteins just happen to be the first 10 stored in the litG graph. As mynodes is a vector that contains one element for each vertex in the litG graph, the number of elements mynodes should be equal to the number of vertices in the litG graph:
> length(mynodes) # Find the number of vertices in the litG graph
[1] 2885
As expected, we find that the litG graph contains 2885 vertices, which represent 2885 different yeast proteins.
Finding the names of proteins that a particular protein interacts with¶
If you are particularly interested in a particular protein in a protein-protein interaction graph, you may want to print out the list of the proteins that that protein interacts with. To do this, you can use the adj() function in the R “graph” package. For example, to print out the proteins that yeast protein YBR009C interacts with in the litG graph, you can type:
> adj(litG, "YBR009C")
$YBR009C
[1] "YBR010W" "YNL031C" "YDR227W"
This tells us that protein YBR009C interacts with three other protein in the litG graph, that is, YBR010W, YNL031C and YDR227W.
Calculating the degree distribution for a graph in R¶
The degree of a vertex (node) in a graph is the number of connections that it has to other vertices in the graph.
The degree distribution for a graph is the distribution of degree values for all the vertices in the graph, that is, the number of vertices in the graph that have degrees of 0, 1, 2, 3, etc.
In terms of a protein-protein interaction graph, each vertex in the graph represents a protein, and the degree of a particular vertex is the number of interactions that that protein has with other proteins.
You can calculate the degrees of all the vertices in a graph by using the degree() function in the R “graph” package. The degree() function returns a vector containing the degrees of each of the vertices in the graph. Remember that there is a degree() function in both the “graph” and “igraph” packages, so if you have loaded both packages, you will need to specify that you want to use the degree() function in the “graph” package, by writing graph::degree().
For example, to calculate the degrees of vertices in the litG graph, we type:
> mydegrees <- graph::degree(litG)
> mydegrees # Print out the values in the vector "mydegrees"
YBL072C YBL083C YBR009C YBR010W YBR031W YBR093C YBR106W YBR118W
0 0 3 3 0 0 0 2
For example, we see from the above results that the yeast protein YBL072C does not interact with any other protein, while the yeast protein YBR118W interacts with two other yeast proteins. Only the first line of the results is shown, as there are 2885 vertices in the litG graph.
You can sort the vector mydegrees in order of the number of degrees, by using the sort() function:
> sort(mydegrees)
YBL072C YBL083C YBR031W YBR093C YBR106W YBR188C YBR191W YBR206W YCL007C YCL018W
0 0 0 0 0 0 0 0 0 0
...
YBR198C YDR392W YDR448W YBR160W YFL039C
8 8 9 10 12
Only the first and last lines of the output are shown above. You can see from the last line of the output that there are some vertices that have high degrees. For example, the vertex corresponding to the protein YFL039C is 12. This means that the protein YFL039C interacts with 12 other proteins. Such highly connected proteins in a protein-protein interaction graph are sometimes called hub proteins.
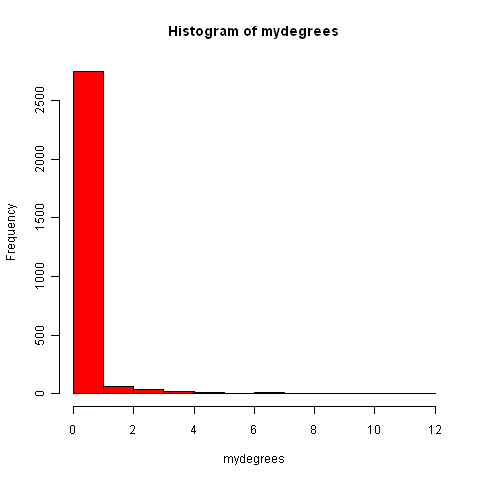
We can calculate the degree distribution for a graph by using the table() function to make a table of how many vertices in the graph have degrees of 0, 1, 2, 3, etc. For example, to calculate the degree distribution for the litG graph, you can type:
> table(mydegrees)
mydegrees
0 1 2 3 4 5 6 7 8 9 10 12
2587 159 58 38 19 7 3 7 4 1 1 1
This tells us that 2587 vertices in the litG graph are not connected to any other vertices, 159 vertices are connected to one other vertex, 58 vertices are connected to two other vertices, and so on. You can calculate the mean degree of the vertices using the mean() function in R:
> mean(mydegrees)
[1] 0.2183709
The mean degree is only about 0.22 for the litG graph, as most of the proteins do not interact with any other protein.
It is nice to visualise the degree distribution for a graph by plotting it as a histogram (using the hist() R function):
> hist(mydegrees, col="red")
Finding connected components in graphs for protein-protein interaction data in R¶
If you are analysing a very large graph, it may contain several subgraphs, where the vertices within each subgraph are connected to each other by edges, but there are no edges connecting the vertices in different subgraphs. In this case, the subgraphs are known as connected components (also called maximally connected subgraphs).
For example, the graph below contains three connected components:
Image source: http://en.wikipedia.org/wiki/Connected_component_(graph_theory)
You can find connected components of a graph in R, by using the connectedComp function in the “RBGL” package. For example, to find connected components in the litG graph, we type:
> library("RBGL")
> myconnectedcomponents <- connectedComp(litG)
The commands above store the connected components in the litG graph in a list myconnectedcomponents. Each connected component is stored in one element of the list variable myconnectedcomponents. That is, each element of the list myconnectedcomponents is a vector containing the names of the proteins in a particular connected component.
We can print out the yeast proteins that are the vertices of the first three connected components by printing out the first three elements in the list myconnectedcomponents. Remember that you need to use double square brackets to access the elements of a list variable in R:
> myconnectedcomponents[[1]]
[1] "YBL072C"
> myconnectedcomponents[[2]]
[1] "YBL083C"
> myconnectedcomponents[[3]]
[1] "YBR009C" "YBR010W" "YNL030W" "YNL031C" "YOL139C" "YAR007C" "YBR073W"
[8] "YER095W" "YJL173C" "YNL312W" "YBL084C" "YDR146C" "YLR127C" "YNL172W"
[15] "YLR134W" "YMR284W" "YER179W" "YIL144W" "YML104C" "YOR191W" "YDL008W"
[22] "YDL030W" "YDL042C" "YDR004W" "YGR162W" "YMR117C" "YDR386W" "YDR485C"
[29] "YDL043C" "YDR118W" "YMR106C" "YML032C" "YDR076W" "YDR180W" "YDL013W"
[36] "YDR227W"
That is, the first two connected components only contain one protein each. These two proteins must not have interactions with any of the other yeast proteins in the litG graph. The third connected component contains 36 proteins. These 36 proteins are not necessarily all connected to each other, but each of the 36 proteins must be connected to at least one of the other 35 proteins in the connected component. Note that the connected components are not stored in the list myconnectedcomponents in any particular order; these just happen to be the first three connected components stored in the list.
To find the total number of connected components in the litG graph, we can just find the length of the list myconnectedcomponents:
> length(myconnectedcomponents)
[1] 2642
That is, there are 2642 different connected components in the litG graph. These are 2642 subgraphs of the graph, where there are edges between the vertices within a subgraph, but no edges between the 2642 subgraphs.
It is interesting to know what is the largest connected component in a graph. How can we calculate this for the litG graph? Well, each element of the litG graph contains a vector storing the proteins in a particular connected component, and the length of this vector is the number of proteins in that connected component. Thus, to calculate the sizes of all connected components in the litG graph, we can use a “for loop” to calculate the length of each of the vectors in myconnectedcomponents in turn:
> componentsizes <- numeric(2642) # Make a vector for storing the sizes of the 2642 connected components
> for (i in 1:2642) {
component <- myconnectedcomponents[[i]] # Store the connected component in a vector "component"
componentsize <- length(component) # Find the number of vertices in this connected component
componentsizes[i] <- componentsize # Store the size of this component
}
In the code above, the line componentsizes <- numeric(2642) makes a new vector componentsizes which has the same number of elements as the number of connected components in the litG graph (2642). This vector componentsizes is then used within the for loop for storing the size of each connected component. We can now find the size of the largest connected component in the litG graph by using the max() R function to find the largest value in the vector componentsizes:
> max(componentsizes)
[1] 88
That is, the largest connected component in the litG graph has 88 different proteins.
We can also use the table() function in R to make a table of the number of connected components of different sizes:
> table(componentsizes)
componentsizes
1 2 3 4 5 6 7 8 12 13 36 88
2587 29 10 7 1 1 2 1 1 1 1 1
This tells us that there is just one connected component with 88 proteins. Furthermore, we see that there are 2587 connected components that contain just 1 protein each. These proteins presumably do not have any known interactions with with any other protein in the litG data set.
To find the connected component that a particular protein belongs to, you can use the findcomponent function:
> findcomponent <- function(graph,vertex)
{
# Function to find the connected component that contains a particular vertex
require("RBGL")
found <- 0
myconnectedcomponents <- connectedComp(graph)
numconnectedcomponents <- length(myconnectedcomponents)
for (i in 1:numconnectedcomponents)
{
componenti <- myconnectedcomponents[[i]]
numvertices <- length(componenti)
for (j in 1:numvertices)
{
vertexj <- componenti[j]
if (vertexj == vertex)
{
found <- 1
return(componenti)
}
}
}
print("ERROR: did not find vertex in the graph")
}
The function findcompontent() returns a vector containing the names of the proteins in the connected component. For example, to find the connected component containing the protein YBR009C, you can type:
> mycomponent <- findcomponent(litG, "YBR009C")
> mycomponent # Print out the members of this connected component.
[1] "YBR009C" "YBR010W" "YNL030W" "YNL031C" "YOL139C" "YAR007C" "YBR073W" "YER095W" "YJL173C" "YNL312W"
[11] "YBL084C" "YDR146C" "YLR127C" "YNL172W" "YLR134W" "YMR284W" "YER179W" "YIL144W" "YML104C" "YOR191W"
[21] "YDL008W" "YDL030W" "YDL042C" "YDR004W" "YGR162W" "YMR117C" "YDR386W" "YDR485C" "YDL043C" "YDR118W"
[31] "YMR106C" "YML032C" "YDR076W" "YDR180W" "YDL013W" "YDR227W"
Extracting a subgraph from a graph in R¶
If you want to extract a particular subgraph of a graph (that is, part of a graph), you can use the subGraph function in the “graph” package. As its arguments (inputs), the subGraph function contains a vector containing the vertices (nodes) in the subgraph that we’re interested in, and the graph that the subgraph belongs to.
For example, if we want to extract the subgraph (of graph litG) that contains the third connected component in the vector myconnectedcomponents, we type:
> myconnectedcomponents <- connectedComp(litG)
> component3 <- myconnectedcomponents[[3]]
> component3 # Print out the proteins in connected component 3
[1] "YBR009C" "YBR010W" "YNL030W" "YNL031C" "YOL139C" "YAR007C" "YBR073W"
[8] "YER095W" "YJL173C" "YNL312W" "YBL084C" "YDR146C" "YLR127C" "YNL172W"
[15] "YLR134W" "YMR284W" "YER179W" "YIL144W" "YML104C" "YOR191W" "YDL008W"
[22] "YDL030W" "YDL042C" "YDR004W" "YGR162W" "YMR117C" "YDR386W" "YDR485C"
[29] "YDL043C" "YDR118W" "YMR106C" "YML032C" "YDR076W" "YDR180W" "YDL013W"
[36] "YDR227W"
> mysubgraph <- subGraph(component3, litG)
> mysubgraph
A graphNEL graph with undirected edges
Number of Nodes = 36
Number of Edges = 48
The commands above store the subgraph corresponding to component3 in a graph object mysubgraph that contains 36 vertices and 48 edges.
Plotting graphs for protein-protein interaction data in R¶
The “Rgraphviz” R package contains useful functions for plotting graphs, or plotting parts of graphs (“subgraphs”).
The layoutGraph and renderGraph functions in the Rgraphviz package can be used to make a nice plot of a subgraph. There are lots of options for the colours to use for plotting vertices and edges.
For example, if we want to make a plot of the subgraph corresponding to the third connected component in the vector myconnectedcomponents, we can type:
> library("Rgraphviz")
> mysubgraph <- subGraph(component3, litG)
> mygraphplot <- layoutGraph(mysubgraph, layoutType="neato")
> renderGraph(mygraphplot)
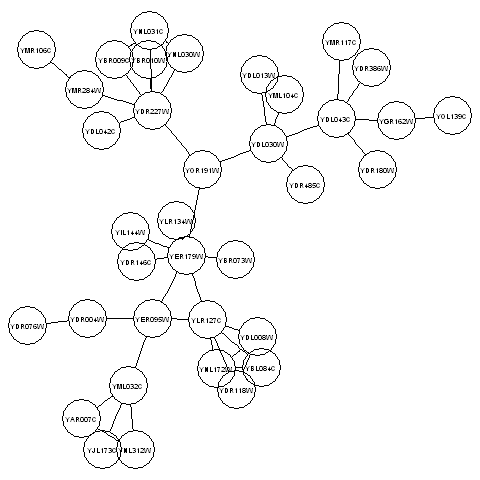
The plot above shows a plot of the third connected component in the graph litG. There are 36 vertices in this subgraph, corresponding to 36 different yeast proteins. The names of the proteins are shown in the circles that represent the vertices. The edges between vertices represent interactions between pairs of proteins.
Detecting communities in a protein-protein interaction graph using R¶
A property common to many types of graphs, including protein-protein interaction graphs, is community structure. A community is often defined as a subset of the vertices in the graph such that connections btween the vertices are denser than connections with the rest of the graph. For example, the graph in the picture below consists of one connected component. However, within that connected component, we can see three densely connected subgraphs; these could be said to be three different communities within the graph:
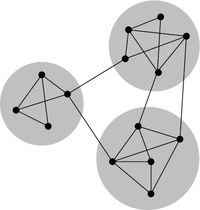
Image source: http://en.wikipedia.org/wiki/Community_structure
In terms of protein-protein interaction networks, if there are several communities within a connected component (for example, three communities, as in the picture above), these could represent three different groups of proteins, where the proteins within one community interact much more with each other than with proteins in the other communities.
By detecting communities within a protein-protein interaction graph, we can detect putative protein complexes, that is, groups of associated proteins that are probably fairly stable over time. In other words, protein complexes can be detected by looking for groups of proteins among which there are many interactions, and where the members of the complex have few interactions with other proteins that do not belong to the complex.
There are lots of different methods available for detecting communities in a graph, and each method will give slightly different results. That is, the particular method used for detecting communities will decide how you split a connected component into one or more communities.
The function findcommunities() below identifies communities within a graph (or subgraph of a graph). It requires a second function, findcommunities2(), which is also below:
> findcommunities <- function(mygraph,minsize)
{
# Function to find network communities in a graph
# Load up the igraph library:
require("igraph")
# Set the counter for the number of communities:
cnt <- 0
# First find the connected components in the graph:
myconnectedcomponents <- connectedComp(mygraph)
# For each connected component, find the communities within that connected component:
numconnectedcomponents <- length(myconnectedcomponents)
for (i in 1:numconnectedcomponents)
{
component <- myconnectedcomponents[[i]]
# Find the number of nodes in this connected component:
numnodes <- length(component)
if (numnodes > 1) # We can only find communities if there is more than one node
{
mysubgraph <- subGraph(component, mygraph)
# Find the communities within this connected component:
# print(component)
myvector <- vector()
mylist <- findcommunities2(mysubgraph,cnt,"FALSE",myvector,minsize)
cnt <- mylist[[1]]
myvector <- mylist[[2]]
}
}
print(paste("There were",cnt,"communities in the input graph"))
}
> findcommunities2 <- function(mygraph,cnt,plot,myvector,minsize)
{
# Function to find network communities in a connected component of a graph
# Find the number of nodes in the input graph
nodes <- nodes(mygraph)
numnodes <- length(nodes)
# Record the vertex number for each vertex name
myvector <- vector()
for (i in 1:numnodes)
{
node <- nodes[i] # "node" is the vertex name, i is the vertex number
myvector[`node`] <- i # Add named element to myvector
}
# Create a graph in the "igraph" library format, with numnodes nodes:
newgraph <- graph.empty(n=numnodes,directed=FALSE)
# First record which edges we have seen already in the "mymatrix" matrix,
# so that we don't add any edge twice:
mymatrix <- matrix(nrow=numnodes,ncol=numnodes)
for (i in 1:numnodes)
{
for (j in 1:numnodes)
{
mymatrix[i,j] = 0
mymatrix[j,i] = 0
}
}
# Now add edges to the graph "newgraph":
for (i in 1:numnodes)
{
node <- nodes[i] # "node" is the vertex name, i is the vertex number
# Find the nodes that this node is joined to:
neighbours <- adj(mygraph, node)
neighbours <- neighbours[[1]] # Get the list of neighbours
numneighbours <- length(neighbours)
if (numneighbours >= 1) # If this node "node" has some edges to other nodes
{
for (j in 1:numneighbours)
{
neighbour <- neighbours[j]
# Get the vertex number
neighbourindex <- myvector[neighbour]
neighbourindex <- neighbourindex[[1]]
# Add a node in the new graph "newgraph" between vertices i and neighbourindex
# In graph "newgraph", the vertices are counted from 0 upwards.
indexi <- i
indexj <- neighbourindex
# If we have not seen this edge already:
if (mymatrix[indexi,indexj] == 0 && mymatrix[indexj,indexi] == 0)
{
mymatrix[indexi,indexj] <- 1
mymatrix[indexj,indexi] <- 1
# Add edges to the graph "newgraph"
newgraph <- add.edges(newgraph, c(i, neighbourindex))
}
}
}
}
# Set the names of the vertices in graph "newgraph":
newgraph <- set.vertex.attribute(newgraph, "name", value=nodes)
# Now find communities in the graph:
communities <- spinglass.community(newgraph)
# Find how many communities there are:
sizecommunities <- communities$csize
numcommunities <- length(sizecommunities)
# Find which vertices belong to which communities:
membership <- communities$membership
# Get the names of vertices in the graph "newgraph":
vertexnames <- get.vertex.attribute(newgraph, "name")
# Print out the vertices belonging to each community:
for (i in 1:numcommunities)
{
cnt <- cnt + 1
nummembers <- 0
printout <- paste("Community",cnt,":")
for (j in 1:length(membership))
{
community <- membership[j]
if (community == i) # If vertex j belongs to the ith community
{
vertexname <- vertexnames[j]
if (plot == FALSE)
{
nummembers <- nummembers + 1
# Print out the vertices belonging to the community
printout <- paste(printout,vertexname)
}
else
{
# Colour in the vertices belonging to the community
myvector[`vertexname`] <- cnt
}
}
}
if (plot == FALSE && nummembers >= minsize)
{
print(printout)
}
}
return(list(cnt,myvector))
}
The function findcommunities() uses the function spinglass.community() from the “igraph” package to identify communities in a graph or subgraph. As its arguments (inputs), the findcommunities() function takes the graph/subgraph that we want to find communities in, and the minimum number of vertices that a community must have to be reported.
For example, to find communities within the subgraph corresponding to the third connected component of the litG graph, we can type:
> mysubgraph <- subGraph(component3, litG)
> findcommunities(mysubgraph, 1)
[1] "Community 1 : YML104C YOR191W YDL030W YDR485C YDL013W"
[1] "Community 2 : YBR073W YDR146C YLR134W YER179W YIL144W"
[1] "Community 3 : YOL139C YGR162W YMR117C YDR386W YDL043C YDR180W"
[1] "Community 4 : YBL084C YLR127C YNL172W YDL008W YDR118W"
[1] "Community 5 : YAR007C YER095W YJL173C YNL312W YDR004W YML032C YDR076W"
[1] "Community 6 : YBR009C YBR010W YNL030W YNL031C YMR284W YDL042C YMR106C YDR227W"
[1] "There were 6 communities in the input graph"
This tells us that there are six different communities in the subgraph corresponding to the third connected component of the litG graph.
Note that if you run findcommunities() again and again on the same input graph, it might find slightly different sets of communities each time. This is because it uses a random number generator in the method that it uses for identifying communities, and the random number used will be different each time you run the findcommunities() function, which means that you will get slightly different answers each time. The answers should be very similar, however, but you might see a small difference, for example, a large community might be split into two smaller communities.
You can make a plot of the communities in a graph or subgraph by using the plotcommunities() function:
> plotcommunities <- function(mygraph)
{
# Function to plot network communities in a graph
# Load the "igraph" package:
require("igraph")
# Make a plot of the graph
graphplot <- layoutGraph(mygraph, layoutType="neato")
renderGraph(graphplot)
# Get the names of the nodes in the graph:
vertices <- nodes(mygraph)
numvertices <- length(vertices)
# Now record the colour of each vertex in a vector "myvector":
myvector <- vector()
colour <- "red"
for (i in 1:numvertices)
{
vertex <- vertices[i]
myvector[`vertex`] <- colour # Add named element to myvector
}
# Set the counter for the number of communities:
cnt <- 0
# First find the connected components in the graph:
myconnectedcomponents <- connectedComp(mygraph)
# For each connected component, find the communities within that connected component:
numconnectedcomponents <- length(myconnectedcomponents)
for (i in 1:numconnectedcomponents)
{
component <- myconnectedcomponents[[i]]
# Find the number of nodes in this connected component:
numnodes <- length(component)
if (numnodes > 1) # We can only find communities if there is more than one node
{
mysubgraph <- subGraph(component, mygraph)
# Find the communities within this connected component:
mylist <- findcommunities2(mysubgraph,cnt,"TRUE",myvector,0)
cnt <- mylist[[1]]
myvector <- mylist[[2]]
}
}
# Get a set of cnt colours, where cnt is equal to the number of communities found:
mycolours <- rainbow(cnt)
# Set the colour of the vertices, so that vertices in each community are of the same colour,
# and vertices in different communities are different colours:
myvector2 <- vector()
for (i in 1:numvertices)
{
vertex <- vertices[i]
community <- myvector[vertex]
mycolour <- mycolours[community]
myvector2[`vertex`] <- mycolour
}
nodeRenderInfo(graphplot) = list(fill=myvector2)
renderGraph(graphplot)
}
For example, to make a plot of the communities in the third connected component of the litG graph using the plotcommunities() function, you need to type:
> mysubgraph <- subGraph(component3, litG)
> plotcommunities(mysubgraph)
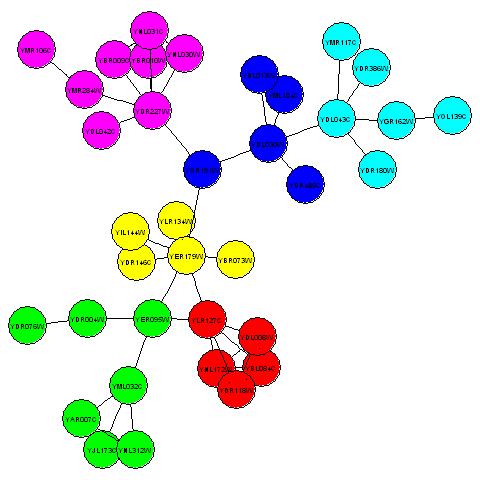
In the graph above, the six communities in the third connected component of the litG graph are coloured with six different colours.
Reading in protein-protein interaction data in R¶
In the above example, you looked at the litG data set of protein-protein interactions, which is a data set that comes with the “yeastExpData” R package. But what if you want to look at a data set of protein-protein interactions that does not come from R?
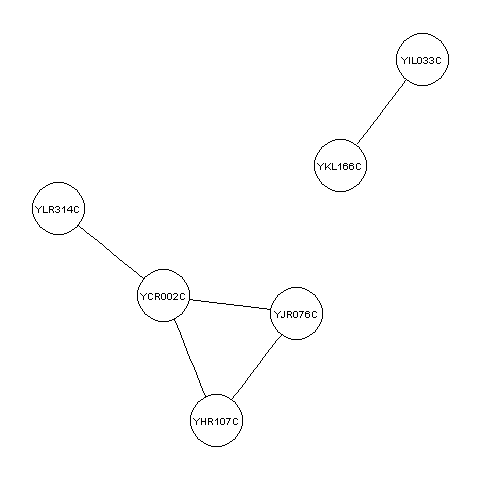
It is common to store data on protein-protein interactions in a text file with two columns, where each line of the file contains a pair of proteins that interact with each other. For example, such a file may look like this: YKL166C YIL033C YCR002C YHR107C YCR002C YJR076C YCR002C YLR314C YJR076C YHR107C This indicates that there are 5 protein-protein interactions, between protein YKL166C and protein YIL033C, between YCR002C and YHR107C, between YCR002C and YJR076C, between YCR002C and YLR314C, and between YJR076C and YHR107C.
The function makeproteingraph() makes a graph based on an input file of protein-protein interactions, where the first two columns of the input file indiciate the pairs of proteins that interact:
> makeproteingraph <- function(myfile)
{
# Function to make a graph based on protein-protein interaction data in an input file
require("graph")
mytable <- read.table(file(myfile)) # Store the data in a data frame
proteins1 <- mytable$V1
proteins2 <- mytable$V2
protnames <- c(levels(proteins1),levels(proteins2))
# Find out how many pairs of proteins there are
numpairs <- length(proteins1)
# Find the unique protein names:
uniquenames <- unique(protnames)
# Make a graph for these proteins with no edges:
mygraph <- new("graphNEL", nodes = uniquenames)
# Add edges to the graph:
# See http://rss.acs.unt.edu/Rdoc/library/graph/doc/graph.pdf for more examples
weights <- rep(1,numpairs)
mygraph2 <- addEdge(as.vector(proteins1),as.vector(proteins2),mygraph,weights)
return(mygraph2)
}
For example, the example file http://www.maths.tcd.ie/~avrillee/littlebookofr/ExampleInteractionData contains the five pairs of interacting proteins listed above. You can read it in and make a graph for these interacting proteins by typing:
> thegraph <- makeproteingraph("http://www.maths.tcd.ie/~avrillee/littlebookofr/ExampleInteractionData")
You can then make a plot of this graph as before:
> mygraphplot <- layoutGraph(thegraph, layoutType="neato")
> renderGraph(mygraphplot)
Creating random graphs in R¶
A random graph is a graph that is generated by a random process, where you start off with a certain number of vertices (nodes), and edges are added by randomly choosing pairs of vertices and making an edge between the two members of each of those pairs of vertices. (This is known as the Erdös-Renyi model for random graphs). In a random graph, vertices with lots of connections are equally likely as vertices with very few connections. That is, if you calculate the average degree of the vertices in a random graph, you will find that the degrees of most of the vertices in the graph is near to the average.
It is often useful and interesting to compare the properties of biological graphs to random graphs. In order to do this, you need to be able to generate some random graphs. The function makerandomgraph() in R makes a random graph with a certain number of edges:
> makerandomgraph <- function(numvertices,numedges)
{
# Function to make a random graph
require("graph")
# Make a vector with the names of the vertices
mynames <- sapply(seq(1,numvertices),toString)
myrandomgraph <- randomEGraph(mynames, edges = numedges)
return(myrandomgraph)
}
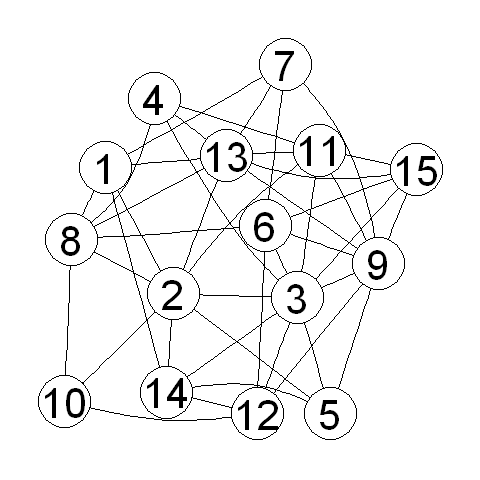
This function takes as its argument (input) the number of vertices and edges that you want the random graph to have to have. For example, to create a random graph that has 15 vertices and 43 edges, we type:
> myrandomgraph <- makerandomgraph(15, 43)
> myrandomgraph # Print out the number of vertices and edges in the graph
A graphNEL graph with undirected edges
Number of Nodes = 15
Number of Edges = 43
In the R code above, we tell R to give the vertices the labels 1 to 15. We can of course plot the random graph:
> myrandomgraphplot <- layoutGraph(myrandomgraph, layoutType="neato")
> renderGraph(myrandomgraphplot)
Summary¶
In this practical, you will have learnt to use the following R functions:
- data() to load a data set that comes with a package into R
- table() for making a table of the data in a vector, or finding out how many elements in a vector have a particular value
- sort() for sorting a vector
All of these functions belong to the standard installation of R.
You have also learnt the following R functions that belong to the additional R packages:
- nodes() from the “graph” package for getting a list of the names of vertices in a graph
- adj() from the “graph” package for getting a list of the vertices that a particular vertex is connected to in a graph
- degree() from the “graph” package for calculating the degree of each of the vertices in a graph
- connectedComp() from the “RBGL” package for identifying connected components in a graph
- subGraph() from the “graph” package for extracting a subgraph from a graph
- layoutGraph() and renderGraph() from the “Rgraphviz” package for plotting a graph or subgraph
Links and Further Reading¶
Some links are included here for further reading.
For background reading on graphs and protein-protein interaction graphs, it is recommended to read Chapters 1, 2 and 4 of Principles of Computational Cell Biology: from protein complexes to cellular networks by Volkhard Helms (Wiley-VCH; http://www.wiley-vch.de/publish/en/books/bySubjectLS00/ISBN3-527-31555-1).
For a more in-depth introduction to R, a good online tutorial is available on the “Kickstarting R” website, cran.r-project.org/doc/contrib/Lemon-kickstart.
There is also a useful introduction to R in Appendix A (“A Brief Introduction to R”) of the book Computational genome analysis: an introduction by Deonier, Tavaré and Waterman (Springer).
There is another nice (slightly more in-depth) tutorial to R available on the “Introduction to R” website, cran.r-project.org/doc/manuals/R-intro.html.
For more in-depth information and more examples on using the “graph” package for analysing graphs, look at the “graph” package documentation, www.cran.r-project.org/web/packages/graph/index.html.
More information and examples on using the “RBGL” package is available in the RBGL documentation at www.cran.r-project.org/web/packages/RBGL/index.html.
More information and examples on using the “Rgraphviz” package is available in the Rgraphviz documentation at www.bioconductor.org/packages/release/bioc/html/Rgraphviz.html.
More information and examples on using the “igraph” package is available in the “igraph” documentation at www.cran.r-project.org/web/packages/igraph/index.html.
There are also very useful chapters on “Using Graphs for Interactome Data” and “Graph Layout” in the book Bioconductor Case Studies by Florian Hahne, Wolfgang Huber, Robert Gentleman and Seth Falcon (http://www.bioconductor.org/pub/biocases/).
Acknowledgements¶
Many of the ideas for the examples and exercises for this practical were inspired by the book Principles of Computational Cell Biology: from protein complexes to cellular networks by Volkhard Helms (Wiley-VCH; http://www.wiley-vch.de/publish/en/books/bySubjectLS00/ISBN3-527-31555-1).
Contact¶
I will be grateful if you will send me (Avril Coghlan) corrections or suggestions for improvements to my email address alc@sanger.ac.uk
License¶
The content in this book is licensed under a Creative Commons Attribution 3.0 License.
Exercises¶
Answer the following questions, using the R package. For each question, please record your answer, and what you typed into R to get this answer.
- Q1. de Lichtenberg et al identified protein-protein complexes in the yeast Saccharomyces cerevisiae that form during the yeast cell cycle. Their data set of pairs of interacting proteins is available for download at the website http://www.cbs.dtu.dk/databases/cellcycle/yeast_complexes/binary_interaction_data.txt. Read this protein-protein interaction data set into R as a graph. How many vertices (proteins) and edges (protein-protein interactions) are there in the graph?
- There are about 6600 predicted genes in the S. cerevisiae genome. Is this the same as the number of vertices in the graph of de Lichtenberg et al‘s data? If not, can you explain why? Note: the full paper by de Lichtenberg et al is available at http://www.sciencemag.org/content/307/5710/724.abstract
- Q2. What is the minimum, maximum and mean number of interactions for the proteins in the graph of de Lichtenberg et al‘s data?
- Can you find an example of a hub protein? Make a histogram plot of the number of interactions for the S. cerevisiae proteins in de Lichtenberg et al‘s data set.
- Q3. Make a random graph with the same number of vertices and edges as the graph of de Lichtenberg et al‘s data. What is the minimum, maximum and mean degree of the vertices for the random graph?
- Is there a difference in the minimum, maximum and mean degree of the vertices for the random graph, when compared to the graph of de Lichtenberg et al‘s data? Compare a histogram plot of the degree distribution for the random graph to a histogram plot of the degree distribution for Lichtenberg et al‘s data set. What do the differences tell you?
- Q4. How many connected components exist in the graph of de Lichtenberg et al‘s data?
- How many connected components just contain 2 proteins? Make a plot of the largest connected component in the graph of de Lichtenberg et al‘s data.
- Q5. What proteins does yeast protein YPR119W interact with, in de Lichtenberg et al‘s data?
- Draw a picture of the connected component that yeast protein YPR119W belongs to. Can you see YPR119W in the picture? Plot the communities in this connected component. Which communities does YPR119W belong to? What protein complex(es) do you think YPR119W belongs to? Can you find anything about the nature of the interactions between YPR119W and the proteins that it interacts with? Hint: search for YPR119W and the proteins that it interacts with in the Saccharomyces Genome Database (www.yeastgenome.org/). It may also be useful to look at Figure 3 in de Lichtenberg et al‘s paper (http://www.sciencemag.org/content/307/5710/724.abstract). Can you identify the complex(es) that YPR119W belongs to in Figure 1 of de Lichtenberg et al‘s paper?
