Hidden Markov Models¶
A little more about R¶
In previous practicals, you learnt how to create different types of variables in R such as scalars, vectors and lists. Sometimes it is useful to create a variable before you actually need to store any data in the variable. To create a vector without actually storing any data in it, you can use the numeric() command to create a vector for storing numbers, or the character() command to create a vector for storing characters (eg. “A”, “hello”, etc.) For example, you may want to create a vector variable for storing the square of a number, and then store numbers in its elements afterwards:
> myvector <- numeric() # Create a vector "myvector" for storing numbers
> for (i in 1:10) { myvector[i] <- i*i } # Fill in the values in the vector "myvector"
> myvector # Print out the vector "myvector"
[1] 1 4 9 16 25 36 49 64 81 100
Note that if you try to store numbers in the elements of a vector that you have not yet created, you will get an error message, for example:
> for (i in 1:10) { avector[i] <- i*i } # Try to store values in the vector "avector"
Error in avector[i] <- i * i : object 'avector' not found
Another very useful type of variable is a matrix. You can create a matrix in R using the matrix() command. If you look at the help page for the matrix() command, you will see that its arguments (inputs) are the data to store in the matrix, the number of rows to store it in, the number of columns to store it in, and whether to fill the matrix with data column-by-column or row-by-row. For example, say you have the heights and weights of eight patients in a hospital in two different vectors:
> heights <- c(180, 170, 175, 160, 183, 177, 179, 182)
> weights <- c(90, 88, 100, 68, 95, 120, 88, 93)
To store this data in a matrix that has one column per person, and one row for heights and one row for weights, we type:
> mymatrix <- matrix(c(heights,weights), 2, 8, byrow=TRUE)
> mymatrix # Print out the matrix
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 180 170 175 160 183 177 179 182
[2,] 90 88 100 68 95 120 88 93
We needed to use the argument “byrow=TRUE” to tell the matrix() command to fill the matrix row-by-row (ie. to put the values from the vector heights into the first row of the matrix, and the values from the vector weights into the second row of the matrix).
You can assign names to the rows and columns of a matrix using the rownames() and colnames() commands, respectively. For example, to assign names to the rows and columns of matrix mymatrix, you could type:
> rownames(mymatrix) <- c("height", "weight")
> colnames(mymatrix) <- c("patient1", "patient2", "patient3", "patient4", "patient5", "patient6", "patient7", "patient8")
> mymatrix # Print out the matrix now
patient1 patient2 patient3 patient4 patient5 patient6 patient7 patient8
height 180 170 175 160 183 177 179 182
weight 90 88 100 68 95 120 88 93
Once you have created a matrix, you can access the values in the elements of the matrix by using square brackets containing the indices of the row and column of the element. For example, if you want to access the value in the second row and fourth column of matrix mymatrix, you can type:
> mymatrix[2,4]
[1] 68
If you want to access all the values in a particular row of the matrix, you can just type the index for the row, and leave out the index for the column. For example, if you want to get the values in the second row of the matrix mymatrix, type:
> mymatrix[2,]
patient1 patient2 patient3 patient4 patient5 patient6 patient7 patient8
90 88 100 68 95 120 88 93
Likewise, if you want to get the values in a particular column of a matrix, leave out the index for the row, and just type the column index. For example, if you want to get the values in the fourth row of the mymatrix, type:
> mymatrix[,4]
height weight
160 68
A multinomial model of DNA sequence evolution¶
The simplest model of DNA sequence evolution assumes that the sequence has been produced by a random process that randomly chose any of the four nucleotides at each position in the sequence, where the probability of choosing any one of the four nucleotides depends on a predetermined probability distribution. That is, the four nucleotides are chosen with pA, pC, pG, and pT respectively. This is known as the multinomial sequence model.
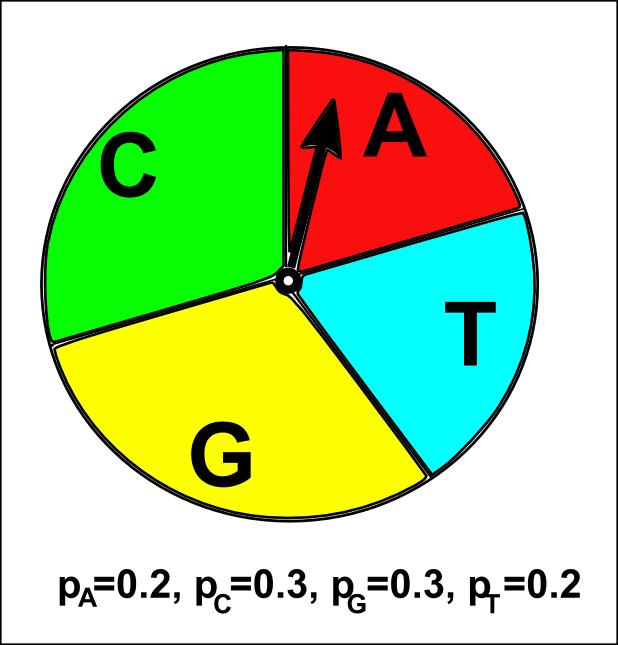
A multinomial model for DNA sequence evolution has four parameters: the probabilities of the four nucleotides pA, pC, pG, and pT. For example, say we may create a multinomial model where pA=0.2, pC=0.3, pG=0.3, and pT=0.2. This means that the probability of choosing a A at any particular sequence position is set to be 0.2, the probability of choosing a C is 0.3, of choosing a G is 0.3, and of choosing a T is 0.2. Note that pA + pC + pG + pT = 1, as the sum of the probabilities of the four different types of nucleotides must be equal to 1, as there are only four possible types of nucleotide.
The multinomial sequence model is like having a roulette wheel that is divided into four different slices labelled “A”, “T”, “G” and “C”, where the pA, pT, pGand pC are the fractions of the wheel taken up by the slices with these four labels. If you spin the arrow attached to the centre of the roulette wheel, the probability that it will stop in the slice with a particular label (eg. the slice labelled “A”) only depends on the fraction of the wheel taken up by that slice (pA here; see the picture below).
Generating a DNA sequence using a multinomial model¶
We can use R to generate a DNA sequence using a particular multinomial model. First we need to set the values of the four parameters of the multinomial model, the probabilities pA, pC, pG, and pT of choosing the nucleotides A, C, G and T, respectively, at a particular position in the DNA sequence. For example, say we decide to set pA=0.2, pC=0.3, pG=0.3, and pT=0.2. We can use the function sample() in R to generate a DNA sequence of a certain length, by selecting a nucleotide at each position according to this probability distribution:
> nucleotides <- c("A", "C", "G", "T") # Define the alphabet of nucleotides
> probabilities1 <- c(0.2, 0.3, 0.3, 0.2) # Set the values of the probabilities
> seqlength <- 30 # Set the length of the sequence
> sample(nucleotides, seqlength, rep=TRUE, prob=probabilities1) # Generate a sequence
[1] "A" "C" "T" "G" "T" "T" "T" "T" "A" "G" "T" "C" "A" "G" "G" "G" "G" "C" "G"
[20] "C" "G" "T" "C" "C" "G" "G" "C" "A" "G" "C"
If you look at the help page for the function(), you will find that its inputs are the vector to sample from (nucleotides here), the size of the sample (seqlength here), and a vector of probabilities for obtaining the elements of the vector being sampled (probabilities1 here). If we use the sample() function to generate a sequence again, it will create a different sequence using the same multinomial model:
> sample(nucleotides, seqlength, rep=TRUE, prob=probabilities1) # Generate another sequence
[1] "T" "G" "C" "T" "A" "T" "G" "G" "T" "C" "G" "A" "A" "T" "G" "G" "G" "G" "C"
[20] "T" "A" "A" "C" "C" "G" "A" "G" "G" "C" "G"
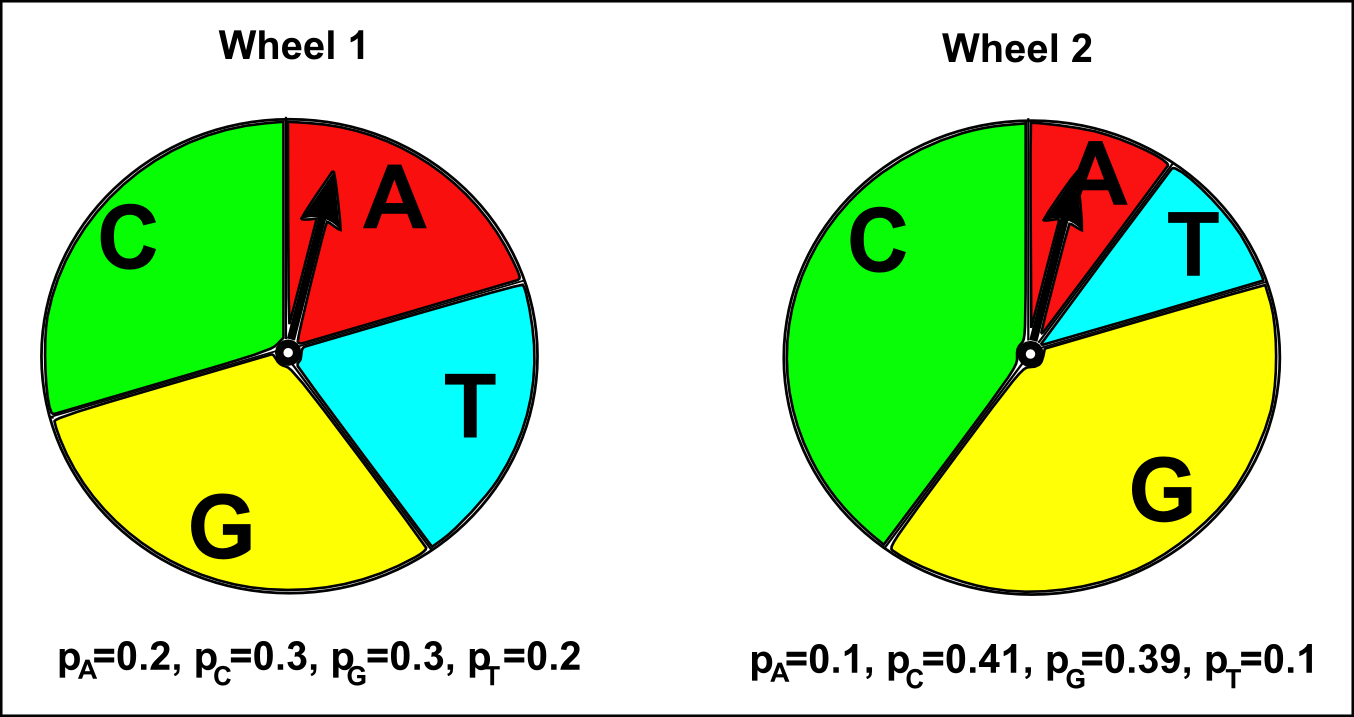
In the same way, we can generate a sequence using a different multinomial model, where pA=0.1, pC=0.41, pG=0.39, and pT=0.1:
> probabilities2 <- c(0.1, 0.41, 0.39, 0.1) # Set the values of the probabilities for the new model
> sample(nucleotides, seqlength, rep=TRUE, prob=probabilities2) # Generate a sequence
[1] "G" "C" "C" "T" "C" "C" "C" "C" "G" "G" "G" "G" "G" "A" "C" "C" "C" "A" "G"
[20] "A" "G" "C" "T" "C" "G" "G" "C" "G" "G" "C"
As you would expect, the sequences generated using this second multinomial model have a higher fraction of Cs and Gs compared to the sequences generated using the first multinomial model above. This is because pC and GT are higher for this second model than for the first model (pC=0.41 and GT=0.39 in the second model, versus pC=0.3 and GT=0.3 in the first model). That is, in the second multinomial model we are using a roulette wheel that has large slices labelled “C” and “G”, while in the first multinomial model we were using a roulette wheel with relatively smaller slices labelled “C” and “G” (see the picture below).
A Markov model of DNA sequence evolution¶
A multinomial model of DNA sequence evolution is a good model of the evolution of many DNA sequences. However, for some DNA sequences, a multinomial model is not an accurate representation of how the sequences have evolved. One reason is that a multinomial model assumes that each part of the sequence (eg. the first 100 nucleotides of the sequence, the second 100 nucleotides, the third 100 nucleotides, etc.) have the same frequency of each type of nucleotide (the same pA, pC, pG, and pT), and this may not be true for a particular DNA sequence if there are considerable differences in nucleotide frequencies in different parts of the sequence.
Another assumption of a multinomial model of DNA sequence evolution is that the probability of choosing a particular nucleotide (eg. “A”) at a particular position in the sequence only depends on the predetermined frequency of that nucleotide (pA here), and does not depend at all on the nucleotides found at adjacent positions in the sequence. This assumption holds true for many DNA sequences. However, for some DNA sequences, it is not true, because the probability of finding a particular nucleotide at a particular position in the sequence does depend on what nucleotides are found at adjacent positions in the sequence. In this case, a different type of DNA sequence model called a Markov sequence model is a more accurate representation of the evolution of the sequence.
A Markov sequence model assumes that the sequence has been produced by a process that chose any of the four nucleotides in the sequence, where the probability of choosing any one of the four nucleotides at a particular position depends on the nucleotide chosen for the previous position. That is, if “A” was chosen at the previous position, then the probability of choosing any one of the four nucleotides at the current position depends on a predetermined probability distribution. That is, given that “A” was chosen at the previous position, the four nucleotides are chosen at the current position with probabilities of pA, pC, pG, and pT of choosing “A”, “C”, “G”, or “T”, respectively (eg. pA=0.2, pC=0.3, pG=0.3, and pT=0.2). In contrast, if “C” was chosen at the previous position, then the probability of choosing any one of the four nucleotides at the current position depends on a different predetermined probability distribution, that is, the probabilities of choosing “A”, “C”, “G”, or “T” at the current position are now different (eg. pA=0.1, pC=0.41, pG=0.39, and pT=0.1).
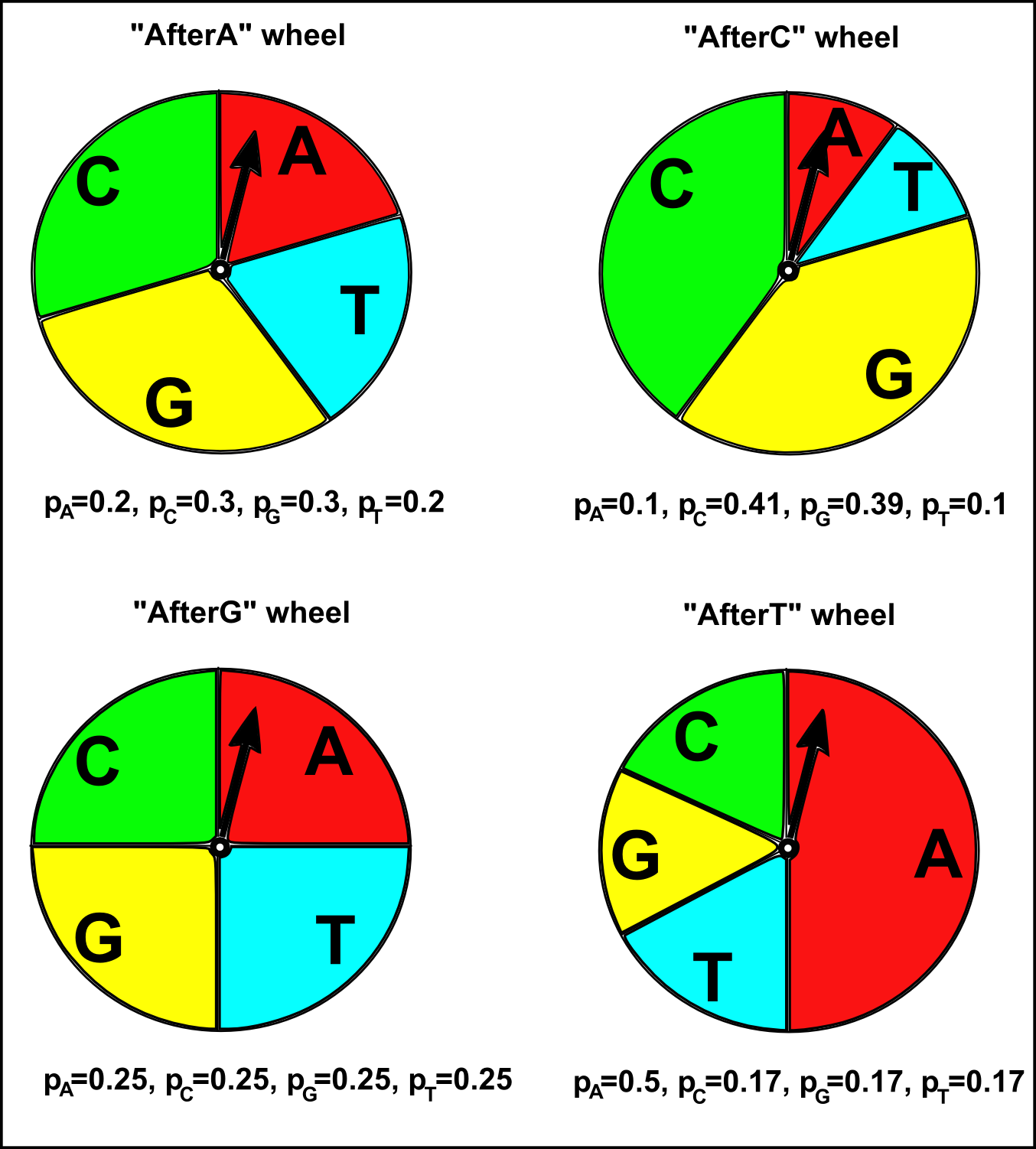
A Markov sequence model is like having four different roulette wheels, labelled “afterA”, “afterT”, “afterG”, and “afterC”, for the cases when “A”, “T”, “G”, or “C” were chosen at the previous position in a sequence, respectively. Each of the four roulette wheels has four slices labelled “A”, “T”, “G”, and “C”, but in each roulette wheel a different fraction of the wheel is taken up by the four slices. That is, each roulette wheel has a different pA, pT, pG and pC. If we are generating a new DNA sequence using a Markov sequence model, to decide what nucleotide to choose at a particular position in the sequence, you spin the arrow at the centre of a roulette wheel, and see in which slice the arrow stops. There are four roulette wheels, and the particular roulette wheel we use at a particular position in the sequence depends on the nucleotide chosen for the previous position in the sequence. For example, if “T” was chosen at the previous position, we use the “afterT” roulette wheel to choose the nucleotide for the current position. The probability of choosing a particular nucleotide at the current position (eg. “A”) then depends on the fraction of the “afterT” roulette wheel taken up by the the slice labelled with that nucleotide (pA here; see the picture below).
The transition matrix for a Markov model¶
A multinomial model of DNA sequence evolution just has four parameters: the probabilities pA, pC, pG, and pT. In contrast, a Markov model has many more parameters: four sets of probabilities pA, pC, pG, and pT, that differ according to whether the previous nucleotide was “A”, “G”, “T” or “C”. The symbols pAA, pAC, pAG, and pAT are usually used to represent the four probabilities for the case where the previous nucleotide was “A”, the symbols pCA, pCC, pCG, and pCT for the case when the previous nucleotide was “C”, and so on.
It is common to store the probability parameters for a Markov model of a DNA sequence in a square matrix, which is known as a Markov transition matrix. The rows of the transition matrix represent the nucleotide found at the previous position in the sequence, while the columns represent the nucleotides that could be found at the current position in the sequence. In R, you can create a matrix using the matrix() command, and the rownames() and colnames() functions can be used to label the rows and columns of the matrix. For example, to create a transition matrix, we type:
> nucleotides <- c("A", "C", "G", "T") # Define the alphabet of nucleotides
> afterAprobs <- c(0.2, 0.3, 0.3, 0.2) # Set the values of the probabilities, where the previous nucleotide was "A"
> afterCprobs <- c(0.1, 0.41, 0.39, 0.1) # Set the values of the probabilities, where the previous nucleotide was "C"
> afterGprobs <- c(0.25, 0.25, 0.25, 0.25) # Set the values of the probabilities, where the previous nucleotide was "G"
> afterTprobs <- c(0.5, 0.17, 0.17, 0.17) # Set the values of the probabilities, where the previous nucleotide was "T"
> mytransitionmatrix <- matrix(c(afterAprobs, afterCprobs, afterGprobs, afterTprobs), 4, 4, byrow = TRUE) # Create a 4 x 4 matrix
> rownames(mytransitionmatrix) <- nucleotides
> colnames(mytransitionmatrix) <- nucleotides
> mytransitionmatrix # Print out the transition matrix
A C G T
A 0.20 0.30 0.30 0.20
C 0.10 0.41 0.39 0.10
G 0.25 0.25 0.25 0.25
T 0.50 0.17 0.17 0.17
Rows 1, 2, 3 and 4 of the transition matrix give the probabilities pA, pC, pG, and pT for the cases where the previous nucleotide was “A”, “C”, “G”, or “T”, respectively. That is, the element in a particular row and column of the transition matrix (eg. the row for “A”, column for “C”) holds the probability (pAC) of choosing a particular nucleotide (“C”) at the current position in the sequence, given that was a particular nucleotide (“A”) at the previous position in the sequence.
Generating a DNA sequence using a Markov model¶
Just as you can generate a DNA sequence using a particular multinomial model, you can generate a DNA sequence using a particular Markov model. When you are generating a DNA sequence using a Markov model, the nucleotide chosen at each position at the sequence depends on the nucleotide chosen at the previous position. As there is no previous nucleotide at the first position in the new sequence, we need to define the probabilities of choosing “A”, “C”, “G” or “T” for the first position. The symbols ΠA, ΠC, ΠG, and ΠT are used to represent the probabilities of choosing “A”, “C”, “G”, or “T” at the first position.
We can define an R function generatemarkovseq() to generate a DNA sequence using a particular Markov model:
> generatemarkovseq <- function(transitionmatrix, initialprobs, seqlength)
{
nucleotides <- c("A", "C", "G", "T") # Define the alphabet of nucleotides
mysequence <- character() # Create a vector for storing the new sequence
# Choose the nucleotide for the first position in the sequence:
firstnucleotide <- sample(nucleotides, 1, rep=TRUE, prob=initialprobs)
mysequence[1] <- firstnucleotide # Store the nucleotide for the first position of the sequence
for (i in 2:seqlength)
{
prevnucleotide <- mysequence[i-1] # Get the previous nucleotide in the new sequence
# Get the probabilities of the current nucleotide, given previous nucleotide "prevnucleotide":
probabilities <- transitionmatrix[prevnucleotide,]
# Choose the nucleotide at the current position of the sequence:
nucleotide <- sample(nucleotides, 1, rep=TRUE, prob=probabilities)
mysequence[i] <- nucleotide # Store the nucleotide for the current position of the sequence
}
return(mysequence)
}
The function generatemarkovseq() takes as its arguments (inputs) the transition matrix for the particular Markov model; a vector containing the values of ΠA, ΠC, ΠG, and ΠT; and the length of the DNA sequence to be generated.
The probabilities of choosing each of the four nucleotides at the first position in the sequence are ΠA, ΠC, ΠG, and ΠT. The probabilities of choosing each of the four nucleotides at the second position in the sequence depend on the particular nucleotide that was chosen at the first position in the sequence. The probabilities of choosing each of the four nucleotides at the third position depend on the nucleotide chosen at the second position, and so on.
We can use the generatemarkovseq() function to generate a sequence using a particular Markov model. For example, to create a sequence of 30 nucleotides using the Markov model described in the transition matrix mytransitionmatrix, using uniform starting probabilities (ie. ΠA = 0.25, ΠC = 0.25, ΠG = 0.25, and ΠT = 0.25) , we type:
> myinitialprobs <- c(0.25, 0.25, 0.25, 0.25)
> generatemarkovseq(mytransitionmatrix, myinitialprobs, 30)
[1] "A" "T" "C" "G" "G" "G" "G" "A" "T" "A" "T" "A" "T" "A" "G" "C" "G" "C" "T" "C" "C" "C" "G"
[24] "A" "C" "A" "A" "A" "T" "C"
As you can see, there are many “A”s after “T”s in the sequence. This is because pTA has a high value (0.5) in the Markov transition matrix mytransitionmatrix. Similarly, there are few “A”s or “T”s after “C”s, which is because pCA and pCT have low values (0.1) in this transition matrix.
A Hidden Markov Model of DNA sequence evolution¶
In a Markov model, the nucleotide at a particular position in a sequence depends on the nucleotide found at the previous position. In contrast, in a Hidden Markov model (HMM), the nucleotide found at a particular position in a sequence depends on the state at the previous nucleotide position in the sequence. The state at a sequence position is a property of that position of the sequence, for example, a particular HMM may model the positions along a sequence as belonging to either one of two states, “GC-rich” or “AT-rich”. A more complex HMM may model the positions along a sequence as belonging to many different possible states, such as “promoter”, “exon”, “intron”, and “intergenic DNA”.
A HMM is like having several different roulette wheels, one roulette wheel for each state in the HMM, for example, a “GC-rich” and an “AT-rich” roulette wheel. Each of the roulette wheels has four slices labelled “A”, “T”, “G”, and “C”, and in each roulette wheel a different fraction of the wheel is taken up by the four slices. That is, the “GC-rich” and “AT-rich” roulette wheels have different pA, pT, pG and pC values. If we are generating a new DNA sequence using a HMM, to decide what nucleotide to choose at a particular sequence position, we spin the arrow of a particular roulette wheel, and see in which slice it stops.
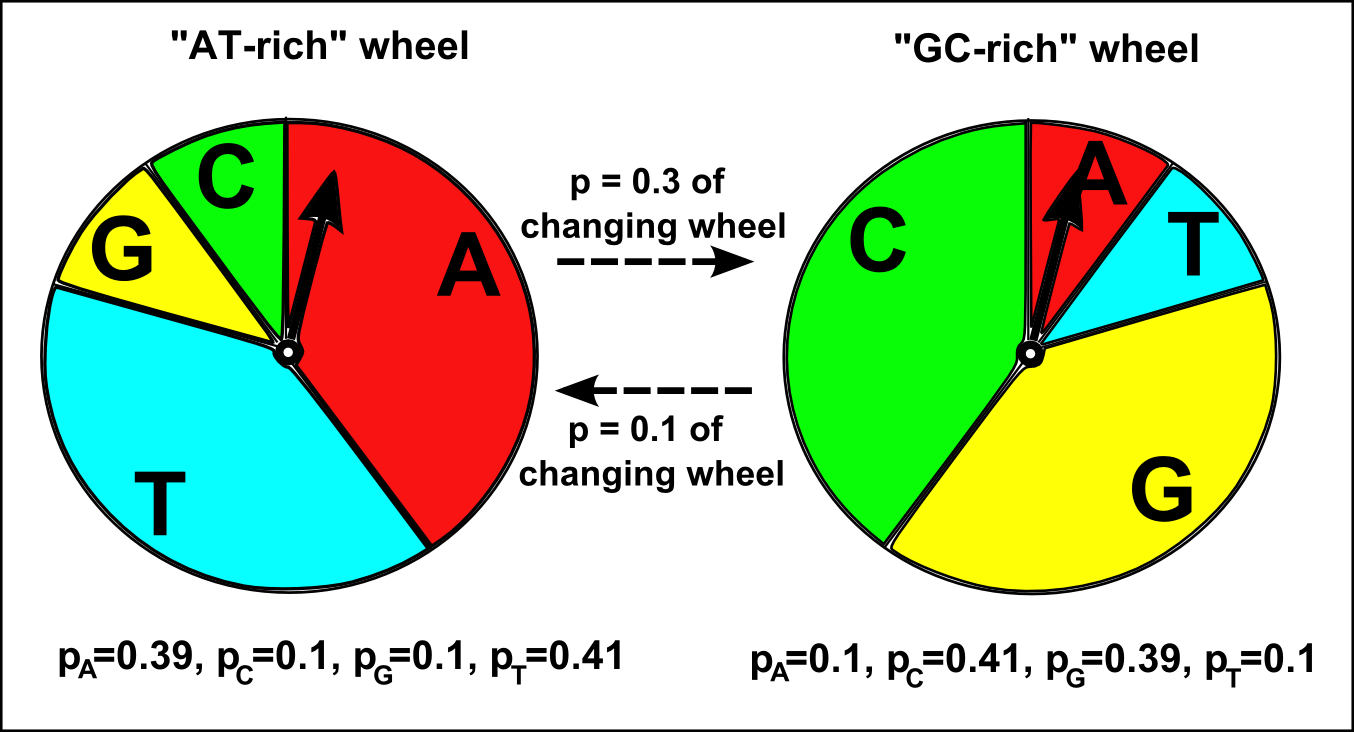
How do we decide which roulette wheel to use? Well, if there are two roulette wheels, we tend to use the same roulette wheel that we used to choose the previous nucleotide in the sequence, but there is also a certain small probability of switching to the other roulette wheel. For example, if we used the “GC-rich” roulette wheel to choose the previous nucleotide in the sequence, there may be a 90% chance that we will use the “GC-rich” roulette wheel again to choose the nucleotide at the current position, but a 10% chance that we will switch to using the “AT-rich” roulette wheel to choose the nucleotide at the current position. Likewise, if we used the “AT-rich” roulette wheel to choose the nucleotide at the previous position, there may be 70% chance that we will use the “AT-rich” wheel again at this position, but a 30% chance that we will switch to using the “GC-rich” roulette wheel to choose the nucleotide at this position.
The transition matrix and emission matrix for a HMM¶
A HMM has two important matrices that hold its parameters. The first is the HMM transition matrix, which contains the probabilities of switching from one state to another. For example, in a HMM with two states, an AT-rich state and a GC-rich state, the transition matrix will hold the probabilities of switching from the AT-rich state to the GC-rich state, and of switching from the GC-rich state to the AT-rich state. For example, if the previous nucleotide was in the AT-rich state there may be a probability of 0.3 that the current nucleotide will be in the GC-rich state, and if the previous nucleotide was in the GC-rich state there may be a probability of 0.1 that the current nucleotide will be in the AT-rich state:
> states <- c("AT-rich", "GC-rich") # Define the names of the states
> ATrichprobs <- c(0.7, 0.3) # Set the probabilities of switching states, where the previous state was "AT-rich"
> GCrichprobs <- c(0.1, 0.9) # Set the probabilities of switching states, where the previous state was "GC-rich"
> thetransitionmatrix <- matrix(c(ATrichprobs, GCrichprobs), 2, 2, byrow = TRUE) # Create a 2 x 2 matrix
> rownames(thetransitionmatrix) <- states
> colnames(thetransitionmatrix) <- states
> thetransitionmatrix # Print out the transition matrix
AT-rich GC-rich
AT-rich 0.7 0.3
GC-rich 0.1 0.9
There is a row in the transition matrix for each of the possible states at the previous position in the nucleotide sequence. For example, in this transition matrix, the first row corresponds to the case where the previous position was in the “AT-rich” state, and the second row corresponds to the case where the previous position was in the “GC-rich” state. The columns give the probabilities of switching to different states at the current position. For example, the value in the second row and first column of the transition matrix above is 0.1, which is the probability of switching to the AT-rich state, if the previous position of the sequence was in the GC-rich state.
The second important matrix is the HMM emission matrix, which holds the probabilities of choosing the four nucleotides “A”, “C”, “G”, and “T”, in each of the states. In a HMM with an AT-rich state and a GC-rich state, the emission matrix will hold the probabilities of choosing each of the four nucleotides “A”, “C”, “G” and “T” in the AT-rich state (for example, pA=0.39, pC=0.1, pG=0.1, and pT=0.41 for the AT-rich state), and the probabilities of choosing “A”, “C”, “G”, and “T” in the GC-rich state (for example, pA=0.1, pC=0.41, pG=0.39, and pT=0.1 for the GC-rich state).
> nucleotides <- c("A", "C", "G", "T") # Define the alphabet of nucleotides
> ATrichstateprobs <- c(0.39, 0.1, 0.1, 0.41) # Set the values of the probabilities, for the AT-rich state
> GCrichstateprobs <- c(0.1, 0.41, 0.39, 0.1) # Set the values of the probabilities, for the GC-rich state
> theemissionmatrix <- matrix(c(ATrichstateprobs, GCrichstateprobs), 2, 4, byrow = TRUE) # Create a 2 x 4 matrix
> rownames(theemissionmatrix) <- states
> colnames(theemissionmatrix) <- nucleotides
> theemissionmatrix # Print out the emission matrix
A C G T
AT-rich 0.39 0.10 0.10 0.41
GC-rich 0.10 0.41 0.39 0.10
There is a row in the emission matrix for each possible state, and the columns give the probabilities of choosing each of the four possible nucleotides when in a particular state. For example, the value in the second row and third column of the emission matrix above is 0.39, which is the probability of choosing a “G” when in the “GC-rich state” (ie. when using the “GC-rich” roulette wheel).
Generating a DNA sequence using a HMM¶
The following function generatehmmseq() can be used to generate a DNA sequence using a particular HMM. As its arguments (inputs), it requires the parameters of the HMM: the HMM transmission matrix and HMM emission matrix.
> # Function to generate a DNA sequence, given a HMM and the length of the sequence to be generated.
generatehmmseq <- function(transitionmatrix, emissionmatrix, initialprobs, seqlength)
{
nucleotides <- c("A", "C", "G", "T") # Define the alphabet of nucleotides
states <- c("AT-rich", "GC-rich") # Define the names of the states
mysequence <- character() # Create a vector for storing the new sequence
mystates <- character() # Create a vector for storing the state that each position in the new sequence
# was generated by
# Choose the state for the first position in the sequence:
firststate <- sample(states, 1, rep=TRUE, prob=initialprobs)
# Get the probabilities of the current nucleotide, given that we are in the state "firststate":
probabilities <- emissionmatrix[firststate,]
# Choose the nucleotide for the first position in the sequence:
firstnucleotide <- sample(nucleotides, 1, rep=TRUE, prob=probabilities)
mysequence[1] <- firstnucleotide # Store the nucleotide for the first position of the sequence
mystates[1] <- firststate # Store the state that the first position in the sequence was generated by
for (i in 2:seqlength)
{
prevstate <- mystates[i-1] # Get the state that the previous nucleotide in the sequence was generated by
# Get the probabilities of the current state, given that the previous nucleotide was generated by state "prevstate"
stateprobs <- transitionmatrix[prevstate,]
# Choose the state for the ith position in the sequence:
state <- sample(states, 1, rep=TRUE, prob=stateprobs)
# Get the probabilities of the current nucleotide, given that we are in the state "state":
probabilities <- emissionmatrix[state,]
# Choose the nucleotide for the ith position in the sequence:
nucleotide <- sample(nucleotides, 1, rep=TRUE, prob=probabilities)
mysequence[i] <- nucleotide # Store the nucleotide for the current position of the sequence
mystates[i] <- state # Store the state that the current position in the sequence was generated by
}
for (i in 1:length(mysequence))
{
nucleotide <- mysequence[i]
state <- mystates[i]
print(paste("Position", i, ", State", state, ", Nucleotide = ", nucleotide))
}
}
When you are generating a DNA sequence using a HMM, the nucleotide is chosen at each position depending on the state at the previous position in the sequence. As there is no previous nucleotide at the first position in the sequence, the function generatehmmseq() also requires the probabilities of the choosing each of the states at the first position (eg. ΠAT-rich and ΠGC-rich being the probability of the choosing the “AT-rich” or “GC-rich” states at the first position for a HMM with these two states).
We can use the generatehmmseq() function to generate a sequence using a particular HMM. For example, to create a sequence of 30 nucleotides using the HMM with “AT-rich” and “GC-rich” states described in the transition matrix thetransitionmatrix, the emission matrix theemissionmatrix, and uniform starting probabilities (ie. ΠAT-rich = 0.5, ΠGC-rich = 0.5), we type:
> theinitialprobs <- c(0.5, 0.5)
> generatehmmseq(thetransitionmatrix, theemissionmatrix, theinitialprobs, 30)
[1] "Position 1 , State AT-rich , Nucleotide = A"
[1] "Position 2 , State AT-rich , Nucleotide = A"
[1] "Position 3 , State AT-rich , Nucleotide = G"
[1] "Position 4 , State AT-rich , Nucleotide = C"
[1] "Position 5 , State AT-rich , Nucleotide = G"
[1] "Position 6 , State AT-rich , Nucleotide = T"
[1] "Position 7 , State GC-rich , Nucleotide = G"
[1] "Position 8 , State GC-rich , Nucleotide = G"
[1] "Position 9 , State GC-rich , Nucleotide = G"
[1] "Position 10 , State GC-rich , Nucleotide = G"
[1] "Position 11 , State GC-rich , Nucleotide = C"
[1] "Position 12 , State GC-rich , Nucleotide = C"
[1] "Position 13 , State GC-rich , Nucleotide = C"
[1] "Position 14 , State GC-rich , Nucleotide = C"
[1] "Position 15 , State GC-rich , Nucleotide = G"
[1] "Position 16 , State GC-rich , Nucleotide = G"
[1] "Position 17 , State GC-rich , Nucleotide = C"
[1] "Position 18 , State GC-rich , Nucleotide = G"
[1] "Position 19 , State GC-rich , Nucleotide = A"
[1] "Position 20 , State GC-rich , Nucleotide = C"
[1] "Position 21 , State GC-rich , Nucleotide = A"
[1] "Position 22 , State AT-rich , Nucleotide = T"
[1] "Position 23 , State GC-rich , Nucleotide = G"
[1] "Position 24 , State GC-rich , Nucleotide = G"
[1] "Position 25 , State GC-rich , Nucleotide = G"
[1] "Position 26 , State GC-rich , Nucleotide = G"
[1] "Position 27 , State GC-rich , Nucleotide = T"
[1] "Position 28 , State GC-rich , Nucleotide = G"
[1] "Position 29 , State GC-rich , Nucleotide = T"
[1] "Position 30 , State GC-rich , Nucleotide = C"
As you can see, the nucleotides generated by the GC-rich state are mostly but not all “G”s and “C”s (because of the high values of pG and pC for the GC-rich state in the HMM emission matrix), while the nucleotides generated by the AT-rich state are mostly but not all “A”s and “T”s (because of the high values of pT and pA for the AT-rics state in the HMM emission matrix).
Furthermore, there tends to be runs of nucleotides that are either all in the GC-rich state or all in the AT-rich state, as the transition matrix specifies that the probabilities of switching from the AT-rich to GC-rich state (probability 0.3), or GC-rich to AT-rich state (probability 0.1) are relatively low.
Inferring the states of a HMM that generated a DNA sequence¶
If we have a HMM with two states, “GC-rich” and “AT-rich”, and we know the transmission and emission matrices of the HMM, can we take some new DNA sequence, and figure out which state (GC-rich or AT-rich) is the most likely to have generated each nucleotide position in that DNA sequence? This is a common problem in bioinformatics. It is called the problem of finding the most probable state path, as it essentially consists of assigning the most likely state to each position in the DNA sequence. The problem of finding the most probable state path is also sometimes called segmentation. For example, give a DNA sequence of 1000 nucleotides, you may wish to use your HMM to segment the sequence into blocks that were probably generated by the “GC-rich” state or by the “AT-rich” state.
The problem of finding the most probable state path given a HMM and a sequence (ie. the problem of segmenting a sequence using a HMM), can be solved by an algorithm called the Viterbi algorithm. As its output, the Viterbi algorithm gives for each nucleotide position in a DNA sequence, the state of your HMM that most probably generated the nucleotide in that position. For example, if you segmented a particular DNA sequence of 1000 nucleotides using a HMM with “AT-rich” and “GC-rich” states, the Viterbi algorithm may tell you that nucleotides 1-343 were most probably generated by the AT-rich state, nucleotides 344-900 were most probably generated by the GC-rich state, and 901-1000 were most probably generated by the AT-rich state.
The following function viterbi() is a function for the Viterbi algorithm:
> viterbi <- function(sequence, transitionmatrix, emissionmatrix)
# This carries out the Viterbi algorithm.
# Adapted from "Applied Statistics for Bioinformatics using R" by Wim P. Krijnen, page 209
# ( cran.r-project.org/doc/contrib/Krijnen-IntroBioInfStatistics.pdf )
{
# Get the names of the states in the HMM:
states <- rownames(theemissionmatrix)
# Make the Viterbi matrix v:
v <- makeViterbimat(sequence, transitionmatrix, emissionmatrix)
# Go through each of the rows of the matrix v (where each row represents
# a position in the DNA sequence), and find out which column has the
# maximum value for that row (where each column represents one state of
# the HMM):
mostprobablestatepath <- apply(v, 1, function(x) which.max(x))
# Print out the most probable state path:
prevnucleotide <- sequence[1]
prevmostprobablestate <- mostprobablestatepath[1]
prevmostprobablestatename <- states[prevmostprobablestate]
startpos <- 1
for (i in 2:length(sequence))
{
nucleotide <- sequence[i]
mostprobablestate <- mostprobablestatepath[i]
mostprobablestatename <- states[mostprobablestate]
if (mostprobablestatename != prevmostprobablestatename)
{
print(paste("Positions",startpos,"-",(i-1), "Most probable state = ", prevmostprobablestatename))
startpos <- i
}
prevnucleotide <- nucleotide
prevmostprobablestatename <- mostprobablestatename
}
print(paste("Positions",startpos,"-",i, "Most probable state = ", prevmostprobablestatename))
}
The viterbi() function requires a second function makeViterbimat():
> makeViterbimat <- function(sequence, transitionmatrix, emissionmatrix)
# This makes the matrix v using the Viterbi algorithm.
# Adapted from "Applied Statistics for Bioinformatics using R" by Wim P. Krijnen, page 209
# ( cran.r-project.org/doc/contrib/Krijnen-IntroBioInfStatistics.pdf )
{
# Change the sequence to uppercase
sequence <- toupper(sequence)
# Find out how many states are in the HMM
numstates <- dim(transitionmatrix)[1]
# Make a matrix with as many rows as positions in the sequence, and as many
# columns as states in the HMM
v <- matrix(NA, nrow = length(sequence), ncol = dim(transitionmatrix)[1])
# Set the values in the first row of matrix v (representing the first position of the sequence) to 0
v[1, ] <- 0
# Set the value in the first row of matrix v, first column to 1
v[1,1] <- 1
# Fill in the matrix v:
for (i in 2:length(sequence)) # For each position in the DNA sequence:
{
for (l in 1:numstates) # For each of the states of in the HMM:
{
# Find the probabilility, if we are in state l, of choosing the nucleotide at position in the sequence
statelprobnucleotidei <- emissionmatrix[l,sequence[i]]
# v[(i-1),] gives the values of v for the (i-1)th row of v, ie. the (i-1)th position in the sequence.
# In v[(i-1),] there are values of v at the (i-1)th row of the sequence for each possible state k.
# v[(i-1),k] gives the value of v at the (i-1)th row of the sequence for a particular state k.
# transitionmatrix[l,] gives the values in the lth row of the transition matrix, xx should not be transitionmatrix[,l]?
# probabilities of changing from a previous state k to a current state l.
# max(v[(i-1),] * transitionmatrix[l,]) is the maximum probability for the nucleotide observed
# at the previous position in the sequence in state k, followed by a transition from previous
# state k to current state l at the current nucleotide position.
# Set the value in matrix v for row i (nucleotide position i), column l (state l) to be:
v[i,l] <- statelprobnucleotidei * max(v[(i-1),] * transitionmatrix[,l])
}
}
return(v)
}
Given a HMM, and a particular DNA sequence, you can use the Viterbi function to find the state of that HMM that was most likely to have generated the nucleotide at each position in the DNA sequence:
> myseq <- c("A", "A", "G", "C", "G", "T", "G", "G", "G", "G", "C", "C", "C", "C", "G", "G", "C", "G", "A", "C", "A", "T", "G", "G", "G", "G", "T", "G", "T", "C")
> viterbi(myseq, thetransitionmatrix, theemissionmatrix)
[1] "Positions 1 - 2 Most probable state = AT-rich"
[1] "Positions 3 - 21 Most probable state = GC-rich"
[1] "Positions 22 - 22 Most probable state = AT-rich"
[1] "Positions 23 - 23 Most probable state = GC-rich"
A Hidden Markov Model of protein sequence evolution¶
We have so far talked about using HMMs to model DNA sequence evolution. However, it is of course possible to use HMMs to model protein sequence evolution. When using a HMM to model DNA sequence evolution, we may have states such as “AT-rich” and “GC-rich”. Similarly, when using a HMM to model protein sequence evolution, we may have states such as “hydrophobic” and “hydrophilic”. In a protein HMM with “hydrophilic” and “hydrophilic” states, the “hydrophilic” HMM will have probabilities pA, pR, pC... of choosing each of the 20 amino acids alanine (A), arginine (R), cysteine (C), etc. when in that state. Similarly, the “hydrophilic” state will have different probabilities pA, pR, pC... of choosing each of the 20 amino acids. The probability of choosing a hydrophobic amino acid such as alanine will be higher in the “hydrophobic” state than in the “hydrophilic” state (ie. pA of the “hydrophobic” state will be higher than the pA of of the “hydrophilic” state, where A represents alanine here). A HMM of protein sequence evolution also defines a certain probability of switching from the “hydrophilic” state to the “hydrophobic” state, and a certain probability of switching from the “hydrophobic” state to the “hydrophilic” state.
Summary¶
In this practical, you will have learnt to use the following R functions:
- numeric() for making a vector for storing numbers
- character() for making a vector for storing characters
- matrix() for making a matrix variable
- rownames() for assigning names to the rows of a matrix variable
- colnames() for assigning names to the columns of a matrix variable
- sample() for making a random sample of numbers from a vector of numbers
All of these functions belong to the standard installation of R.
Links and Further Reading¶
Some links are included here for further reading, which will be especially useful if you need to use the R package for your project or assignments.
For background reading on multinomial models, Markov models, and HMMs, it is recommended to read Chapters 1 and 4 of Introduction to Computational Genomics: a case studies approach by Cristianini and Hahn (Cambridge University Press; www.computational-genomics.net/book/).
There is also a very nice chapter on “Markov Models” in the book Applied statistics for bioinformatics using R by Krijnen (available online at cran.r-project.org/doc/contrib/Krijnen-IntroBioInfStatistics.pdf).
Acknowledgements¶
Many of the ideas for the examples and exercises for this practical were inspired by the Matlab case studies on the Bacteriophage lambda genome (www.computational-genomics.net/case_studies//lambdaphage_demo.html) and on the olfactory receptors (www.computational-genomics.net/case_studies/olfactoryreceptors_demo.html) from the website that accompanies the book Introduction to Computational Genomics: a case studies approach by Cristianini and Hahn (Cambridge University Press; www.computational-genomics.net/book/).
Several of the examples and and sample code used in this practical were inspired by the examples and code in the great chapter on “Markov models” in the book Applied statistics for bioinformatics using R by Krijnen (available online at cran.r-project.org/doc/contrib/Krijnen-IntroBioInfStatistics.pdf).
Thank you to Noel O’Boyle for his nice suggestion of using roulette wheels to explain multinomial models, Markov models and HMMs.
Exercises¶
Answer the following questions, using the R package. For each question, please record your answer, and what you typed into R to get this answer.
- Q1. In a previous practical, you saw that the Bacteriophage lambda genome sequence (NCBI accession NC_001416) has
long stretches of either very GC-rich (mostly in the first half of the genome) or very AT-rich sequence (mostly in the second half of the genome). Use a HMM with two different states (“AT-rich” and “GC-rich”) to infer which state of the HMM is most likely to have generated each nucleotide position in the Bacteriophage lambda genome sequence. For the AT-rich state, set pA= 0.27, pC= 0.2084, pG= 0.198, and pT= 0.3236. For the GC-rich state, set pA= 0.2462, pC= 0.2476, pG= 0.2985, and pT= 0.2077. Set the probability of switching from the AT-rich state to the GC-rich state to be 0.0002, and the
probability of switching from the GC-rich state to the AT-rich state to be 0.0002. What is the most probable state path?- Q2. Given a HMM with four different states (“A-rich”, “C-rich”, “G-rich” and “T-rich”), infer which state of
- the HMM is most likely to have generated each nucleotide position in the Bacteriophage lambda genome sequence. For the A-rich state, set pA= 0.3236, pC= 0.2084, pG= 0.198, and pT= 0.27. For the C-rich state, set pA= 0.2462, pC= 0.2985, pG= 0.2476, and pT= 0.2077. For the G-rich state, set pA= 0.2462, pC= 0.2476, pG= 0.2985, and pT= 0.2077. For the T-rich state, set pA= 0.27, pC= 0.2084, pG= 0.198, and pT= 0.3236. Set the probability of switching from the A-rich state to any of the three other states to be 6.666667e-05. Likewise, set the probability of switching from the C-rich/G-rich/T-rich state to any of the three other states to be 6.666667e-05. What is the most probable state path? Do you find differences between these results and the results from simply using a two-state HMM (as in Q1)?
- Q3. Make a two-state HMM to model protein sequence evolution, with “hydrophilic” and “hydrophobic” states.
- For the hydrophilic state, set pA= 0.02, pR= 0.068, pN= 0.068, pD= 0.068, pC= 0.02, pQ= 0.068, pE= 0.068, pG= 0.068, pH= 0.068, pI= 0.012, pL= 0.012, pK= 0.068, pM= 0.02, pF= 0.02, pP= 0.068, pS= 0.068, pT= 0.068, pW= 0.068, pY= 0.068, and pV= 0.012. For the hydrophobic state, set pA= 0.114, pR= 0.007, pN= 0.007, pD= 0.007, pC= 0.114, pQ= 0.007, pE= 0.007, pG= 0.025, pH= 0.007, pI= 0.114, pL= 0.114, pK= 0.007, pM= 0.114, pF= 0.114, pP= 0.025, pS= 0.026, pT= 0.026, pW= 0.025, pY= 0.026, and pV= 0.114. Set the probability of switching from the hydrophilic state to the hydrophobic state to be 0.01. Set the probability of switching from the hydrophobic state to the hydrophilic state to be 0.01. Now infer which state of the HMM is most likely to have generated each amino acid position in the the human odorant receptor 5BF1 protein (UniProt accession Q8NHC7). What is the most probable state path? The odorant receptor is a 7-transmembrane protein, meaning that it crosses the cell membrane seven times. As a consequence the protein has seven hydrophobic regions that cross the fatty cell membrane, and seven hydrophilic segments that touch the watery cytoplasm and extracellular environments. What do you think are the coordinates in the protein of the seven transmembrane regions?